1. 문제

2. 접근 방식
1) nth level에는 n개의 노드가 있다.
2) n level의 i번째노드는 n+1 level의 i번째 노드와 i+1번째 노드만 접근할 수 있다.
3) dp[n][n]구현 : dp[i][j]: i번째 레벨의 j번째 노드를 선택했을 때 얻을 수 있는 최대 비용
dp[i][j] = max(dp[i-1][j-1], dp[i-1][j]) + (i level의 j번째 노드의 값)
4) dp 함수 구현
4-1) bottom-up 방식 : 이중 for문으로 dp[1][1]부터 구하기 시작해서 dp[n][n]까지 구함. 리턴 값은 dp[n][1]~dp[n][n]값들 중 max값
4-2) top-down 방식: 재귀 함수로 구현. 종료 조건( n==0일 때, 이미 dp배열에 값이 이미 저장되었을 때) 구현 필요. dp[i][j]에 새로운 값을 넣은 후, 해당 값을 리턴 함
3. 실수 & 주의 할 점
1) 본의 아니게 greedy로 구현함
- i번째 레벨에서의 최대값 : i-1번째 레벨까지 순회했을 때의 최대 경로 + max(i번째 레벨의 index번째 노드, i번째 레벨의 index+1 번째 노드) .*index: 최대 경로의 i-1레벨 노드 번호
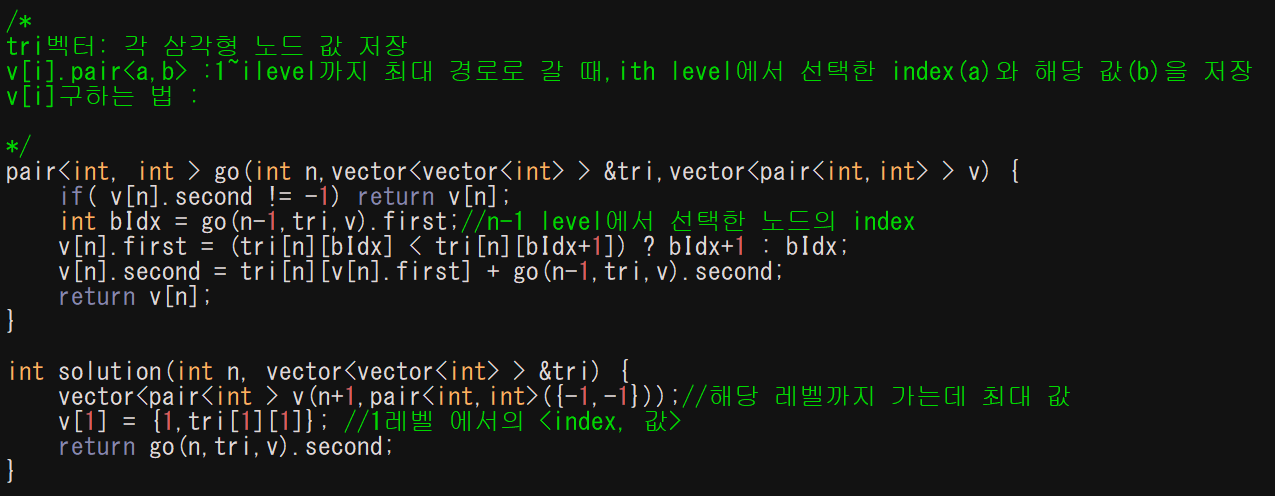
- level별로 구하면 항상 직전 레벨에서 최대값인 경우로만 순회한다. 하지만 직전에선 최대값이 아니지만 현재 노드 값이 매우 큰 경우도 있으므로 이 경우는 greedy로 풀면 안됨.
- 이렇게 구현하는 게 그리디 방식인 걸 인지하기
-> 그리디: 직전 레벨에서의 최대값을 찾은 후, 현재 노드 값 더하기
->DP : (직전 레벨에서 나올 수 있는 경우의 수 + 각 경우의 수에서 접근 할 수 있는 현재 노드 값 ) 중 최대 값
- 대충.. 느낌적으로는 이렇게 차이가 있는 것 같다. 하지만 좀 더 명확하게 그리디 구현 방식과 DP구현 방식에 대해 공부 하기!!
2) 메모리 초과
- 함수의 매개변수로 벡터 쓸 때, 참조로 선언할 것!! (& 잊지 말기)
4. 코드
#include<iostream>
#include<vector>
#include <algorithm>
using namespace std;
int go(int n,int j,vector<vector<int> > &tri,vector<vector<int> > &v) {
if( n == 0 ||j == 0 || j > n ) return 0;
if( v[n][j] != -1) return v[n][j];
v[n][j] = tri[n][j] + max(go(n-1,j-1,tri,v),go(n-1,j,tri,v));
//cout <<"v["<<n<<"]["<<j<<"] = "<<v[n][j]<<endl;
return v[n][j];
}
int solution(int n, vector<vector<int> > &tri) {
vector<vector<int> > v(n+1,vector<int>(n+1,-1));//해당 레벨까지 가는데 최대 값
v[1][1] = tri[1][1];
int ret = -1;
for(int i=1 ; i <=n;i++) {
//cout <<endl<<n<<","<<i<<" 경로 구하기 시작"<<endl;
ret = max(ret, go(n,i,tri,v));
}
return ret;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(NULL);cout.tie(NULL);
int n;
cin >> n;
vector<vector<int> > tri(n+1,vector<int>(n+1,-1));
for(int i=1;i<=n;i++) {
for(int j=1;j<=i;j++) {
cin >> tri[i][j];
}
}
cout << solution(n,tri);
return 0;
}
'알고리즘 > 백준' 카테고리의 다른 글
| [백준] DP (0) | 2020.07.02 |
|---|---|
| [9251] LCS(C++) (0) | 2020.06.26 |
| [백준]수학1 (0) | 2020.06.17 |
| [1010]다리 놓기(C++)/DP (1) | 2020.06.16 |
| [백준] 정렬 (2) | 2020.06.16 |



