[ ✅ 기본 용어 ]
모집단과 표본
1) 모집단(Population) : 통계분석 방법을 적용할 전체 집합
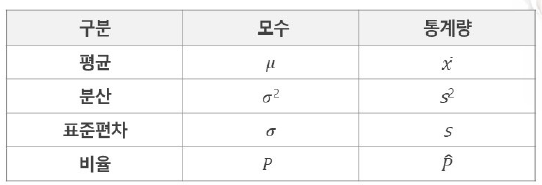
2) 모수(Parameters) : 모집단을 분석하여 얻어지는 결과 수치
3) 표본(Sample) : 직접적인 조사 대상이 된 모집단 일부
4) 통계량(Statistics): 표본을 분석하여 얻어지는 결과
변수

열(세로) = 변수(Variable) = 특성(Feature) = Attribute(속성)
행(가로) = Observation = instance
값 = Label = class = target
데이터 타입(타입 별 어떤 분석 기법을 적용해야 하는가?)

1) 범주형(Categorical Data)
- 정성적, 질적 자료
- 빈도 중심 Numerical 분석
- "빈도 분석" 통계 사용
- 글자
- 분할표, 파이 그래프, 모자이크 plot
- 범주별 출현 빈도에 기반한 분석
- 빈도, 비율, 누적비율 등
- "특정 분포 가정"이 없이 빈도 기반 확률
1- 1) 범주형 : 명목형(Nominal Data)
- 숫자로 바뀌어도 단순히 범주를 표시하는 데이터
- 성별, 혈액형
1-2) 범주형 : 순서형(Ordinal Data)
- 범주 순서가 상대적으로 비교 가능
- 대부분 수치화 자료를 그룹화 하여서 순서화로 바꿈
- 비만도, 학점, 선호도
2) 수치형(Numerical Data)
- 정량적, 양적 자료
- 범위형, 비율형
- 평균 / 분산의 Numerical 분석 가능
- 측정 오차
- "분포 분석" 통계 사용
- 숫자,평균, 분산, 표준편차
- 히스토그램, 상자그림(Box plot), 산점도
- 데이터의 특성을 분포로 설명
- "특정 분포"를 가정하는 경우가 대부분
2-1) 수치형 : 이산형(Discrete Data)
- 셀 수 있는 형태의 자료
- 멤버의 수, 교통사고 건 수
2-2) 수치형 : 연속형(Continuous Data)
- 2-2-1) 등간형(Interval) : 비교할 수 있도록 단위가 정해진 경우, +/- 가능
- 온도, 점수(ex: 20도가 10도보다 두 배 더운 것은 아님)
- 2-2-2) 비율형(Ratio) : 0이없음을 의미하는 경우, 사칙 연산 가능
- 신장, 체중, 매출액, 시청률
데이터 Type별 통계 분석 (중요!!!)
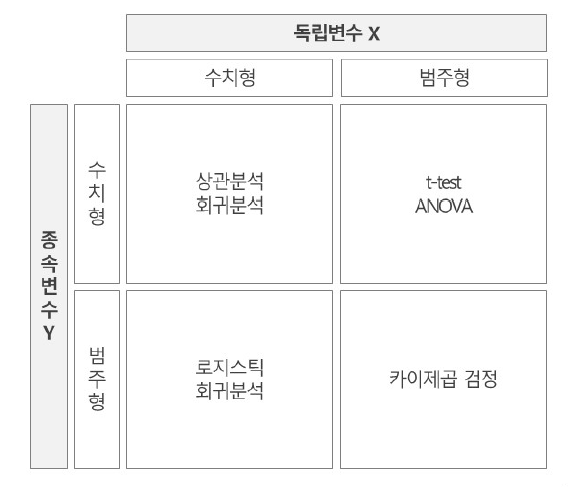
- 중요!! 종속변수에 범주형이 나온다 == "분류 문제"
- X가 수치 & Y가 수치 => 상관분석, 회귀분석
- X가 수치 & Y가 범주 => 로지스틱 회귀분석
[ ✅ 기본 용어 : 시각화 ]


그래프 특징
| 히스토그램 (Histogram) |
표로 되어있는 도수 분포를 정보 그림으로 나타낸 것 |
그룹 존재 유무 이상치 존재 유무 중심값, 대칭 여부 |
가로 = 계급 세로 = 도수 |
| 상자 그림 (Box Plot) |
데이터를 사분위수(Quartile)로 쪼갠것 | 그룹 존재 유무 이상치 존재 유무 최대값, 최소값 확인 폭 : Data분포(data개수가 동일하지만 값 차이가 크다) Box(OQR)에는 전체 데이터의 50% |
모든 데이터가 같은 값을 가지고 있다면, 사분위 수가 1개의 값으로, 선도 1개만 나옴 |
| 산점도 (Scatter Plot) |
데이터를 점으로 표현한 것 | 그룹 존재 유무 이상치 존재 유무 |
데이터 간의 관계성(선형 / 비선형) 알 수 있음 인과관계는 알 수 없음 |
[ ✅ 통계 분석 : 분포 분석 (수치형 변수)]
- 위치 통계량(중심 경향성), 변이 통계량, 모양 통계량으로 크게 분석 가능
- 분포에 대한 가정을 요할 수 있음
- 통계량 : 표본을 분석하여 얻어지는 결과 수치
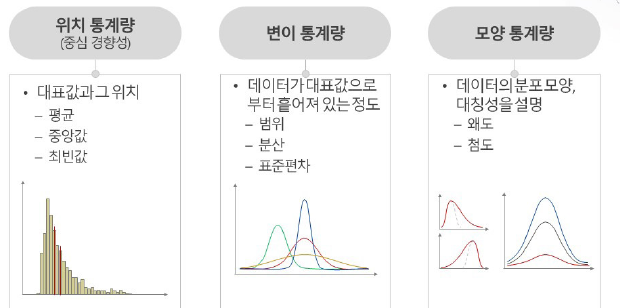
1. 위치 통계량(중심 경향성)
1) 평균
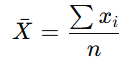
- 각 자료에 대해 유일 값을 가짐
- 통계 분석의 대표값으로 널리 사용
- 극단적인 값에 민감하다
- 자료 수가 적고 극단값이 여러 개일 경우 대푯값의 기능 상실
2) 중앙값(median)
- 데이터를 순서대로 나열할 때 가운데 있는 값
- 홀수 개 : (n+1) / 2
- 짝수 개 : n/2번째와 (n+2)/2 번째 값의 평균
3) 최빈값(mode) (중요!!)
- 빈도가 가장 많은 관측치
- 평균 / 중앙값과 달리 "존재하지 않을 수도 있고, 유일한 값이 아닐 수도 있음"
- 질적 변수에도 활용 가능
4) 중앙값 & 최빈값 특징
- 자료 속에 극단적 이상치가 있음 : 덜 민감한 "중앙값"을 대표값으로 사용
- 자료 분포가 비대칭 : 평균의 보조자료로 이용 가능
- 개방 구간을 갖는 도수 분포표 : 중앙값 또는 최빈값을 대표값으로 사용
- 명목 자료, 서열 자료 : "최빈값"을 대표값으로 사용(중앙값 / 평균을 계산 X)
- 자료 속에 극단적 이상치가 있음 : 덜 민감한 "중앙값"을 대표값으로 사용
5) 팁
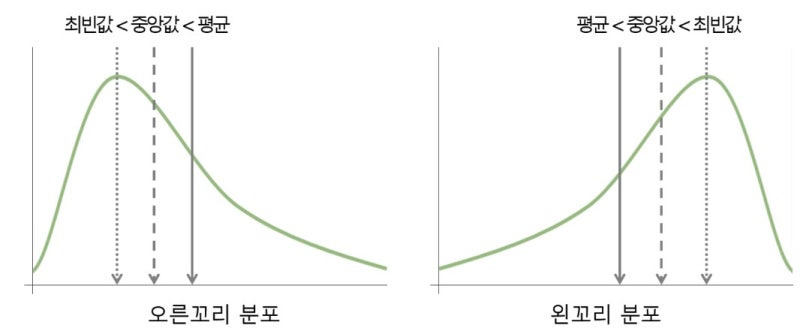
- 오른쪽 꼬리가 긴 분포 : 모(mode) < 메(median) < 민(mean)
- 왼쪽 꼬리가 긴 분포 : 민(mean) < 메(median) < 모(mode)
2. 변이 통계량 (퍼짐 정도)
중심 경향성, 산포도 고려 : 자료가 흩어져 있는 정도를 측정
두 분포에서 자료의 흩어짐을 비교하는데 이용
1) 범위 : 최대값 - 최소값
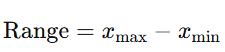
2) 중간 범위 : 최대값 + 최소값 / 2
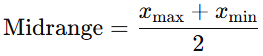
3) 평균절대 편차(Mean Absolute Deviation) : abs|데이터 - 평균값| 의 평균
(편차: 자료에서 각 값이 평균으로부터 떨어진 정도)
(분산 = 편차제곱의 평균)
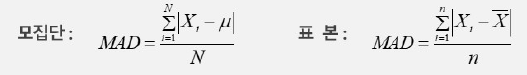
4) 분산 : 편차제곱의 평균
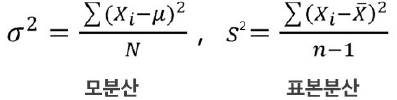
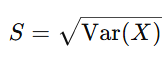
- 중요!!! : "표본"이란 말이 나오면, "분산 & 표준 편차"는 n-1로 나누어야 함
- n-1을 사용해야 모수에 대한 불편추정량(unbiased)
- 불편 추정량 : 어떤 추정량의 기대값이 추정하고자 하는 모수와 같으면 불편추정량
모집단의 참된 값(모수, Parameter)을 추정할 때, 기대값이 해당 모수와 같은 통계량을 의미한다.
분산을 추정할 때, 단순히 n으로 나누면 실제 모집단의 분산보다 값이 작아지는 편향(Bias)이 발생한다.
이를 보정하기 위해 n−1로 나누면, 기대값이 실제 모집단 분산과 동일해져서 불편한(Unbiased) 추정량이 된다.
즉, 표본 분산을 불편하게 만들지 않기 위해 n−1로 나누는 것이다.
4-2) 분산의 특징
- 주어진 자료가 평균 주위로 얼마나 집중되어 있는가
- 분산이 작으면 자료 변동이 심하지 않고, 대체로 평균 가까이에 분포
- 분산은 각 자료에 대한 편차 제곱으로 구함 -> 원자료의 단위와 달라짐!
- n-1을 사용하여 모분산의 불편추정치(unbiased estimator)가 되도록 함
5) 자유도
- 전체 데이터 중 실질적으로 독립적인 데이터 개수
- 자유도 = 자료 개수 - 1(고정은 X)
- 자유도를 고려하지 않은 표준편차 : 실제 값을 "과소 평가" 가능
- 극단적으로 자료 개수가 1개인 경우
- 자유도를 고려하면 계산 불가능 : 자료 하나로부터 퍼진 정도를 알 수 없으므로, 알수 없다가 정답
6) 표준 편차
- 분산의 제곱근
- 표준 편차를 구하면 "원래 자료의 단위로 환원" -> 평균 / 타 통계량과 쉽게 비교 가능
7) 변이 통계량의 특징(중요!!)
- 자료가 흩어짐 => 범위, 중간범위, 분산, 표준 편차는 커짐
- 자료가 모두 동일 => 범위, 중간범위, 분산, 표준편차 0
- 범위, 중간범위, 분산 표준편차 => 모두 "양수"
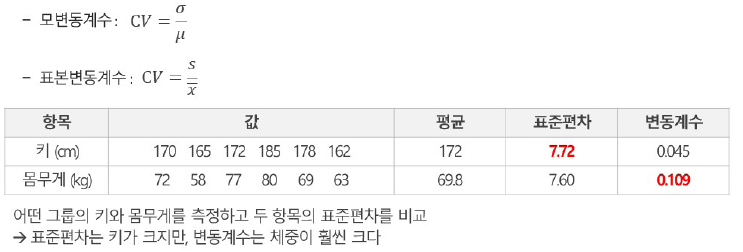
8) 변동 계수(변이 계수) : coefficient of variation
- coefficient of variation (CV) 혹은 상대 표준 편차(relative standard deviation)
- 표준 편차 / 평균
- 서로 다른 데이터 간 편차를 비교하는 법
- 특히, 두 개의 scale이 다를 때 비교 가능
- 같은 항목을 다른 데이터 그룹 간 비교, 다른 항목 비교
- ex) 성별 간의 체중 편차 비교, 키와 체중의 편차 비
3. 모양 통계량(분포의 모양)
Box - Plot
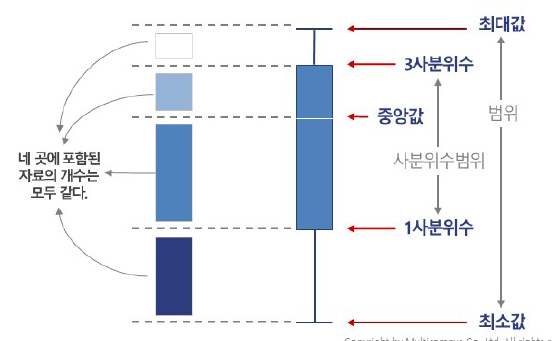
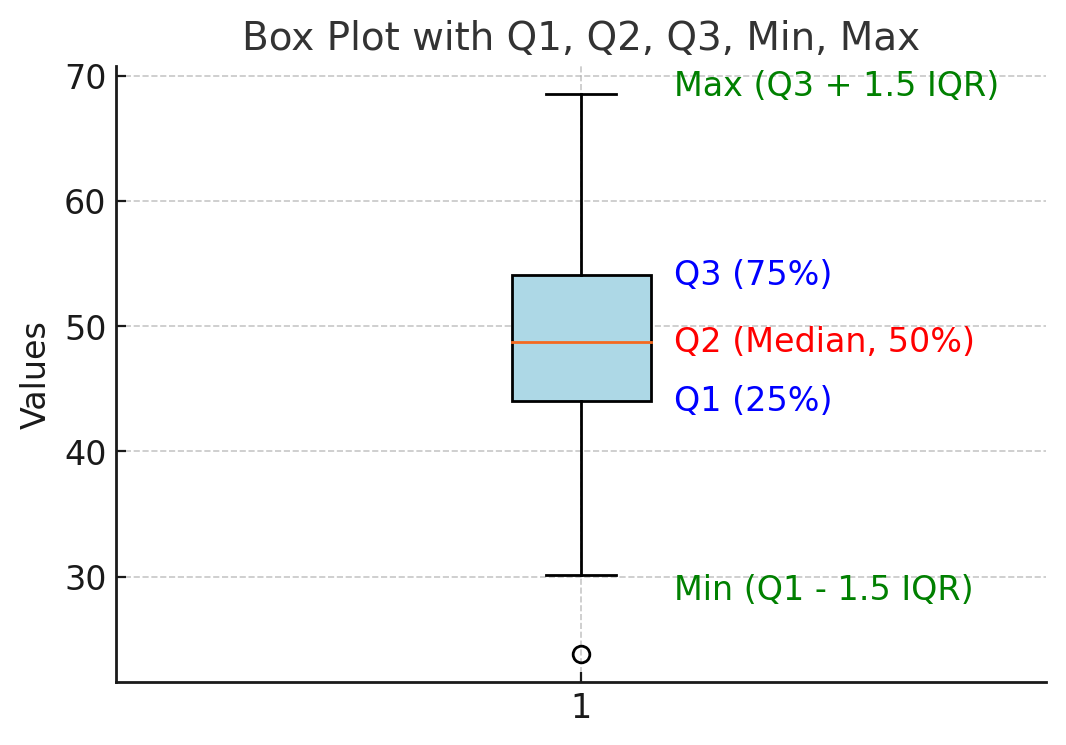
- 최솟값 (Minimum): 이상치를 제외한 데이터 중 가장 작은 값
- 제1사분위수 (Q1, 25th Percentile): 하위 25% 지점
- 중앙값 (Q2, Median, 50th Percentile): 데이터의 정중앙 값
- 제3사분위수 (Q3, 75th Percentile): 상위 25% 지점
- 최댓값 (Maximum): 이상치를 제외한 데이터 중 가장 큰 값
- 이상치 (Outliers): 일반적인 데이터 범위를 벗어난 값
💡 사분위범위 (IQR, Interquartile Range)
사분위범위(IQR)는 데이터의 중앙 50% 범위를 의미하며, 다음과 같이 계산된다.
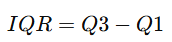

왜도(skewness) / 첨도(kurtosis)
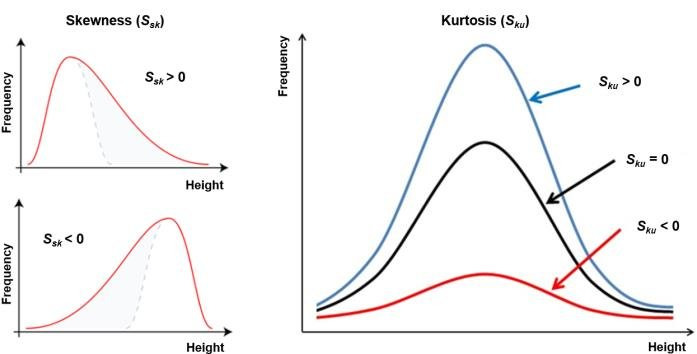
- 왜도 : 자료의 대칭성을 보는 척도
- 오른쪽 꼬리가 긴 분포 : positive
- 첨도 : 정규분포 대비 봉오리의 높이를 알아보는 측도
[ ✅ 통계 분석 : 확률 & 베이즈 정리 ]
1. 확률 실험 / 확률 실행의 조건
- 실험 결과를 알 수 없음
- 결과는 알지 못하지만 결과의 가능한 경우의 수를 알고 있음
- 동일한 실험을 반복 가능
2. 확률 용어
1️⃣ 확률(Probability)
- 특정 사건이 발생할 가능성을 나타내는 값
- 확률의 범위

- 공식

2️⃣ 표본공간(Sample Space, ( S ), 옴 )
- 가능한 모든 결과의 집합
- 예시
- 동전 던지기 → ( S = {H, T} )
- 주사위 던지기 → ( S = {1, 2, 3, 4, 5, 6} )
3️⃣ 사건(Event) : 기호 알파벳 대문자로 표기
- 표본공간의 부분집합
- 근원 사건 : 어떤 사건이 표본 공간 상 하나의 원소로 구성
- 단순 사건(Simple Event): 하나의 결과만 포함
- 복합 사건(Compound Event): 여러 결과를 포함
예시
- 주사위 던지기에서 3이 나오는 사건 → ( A = {3} )
- 짝수가 나오는 사건 → ( B = {2, 4, 6} )




확률의 법칙

3. 조건부 확률

4. 베이즈 정리
- 새로운 정보를 반영하여 확률을 업데이트하는 방법
- 처음에 우리가 가지고 있던 확률(사전 확률)을, 추가적인 정보(가능도)를 이용해 수정하여 새로운 확률(사후 확률)을 계산하는 과정
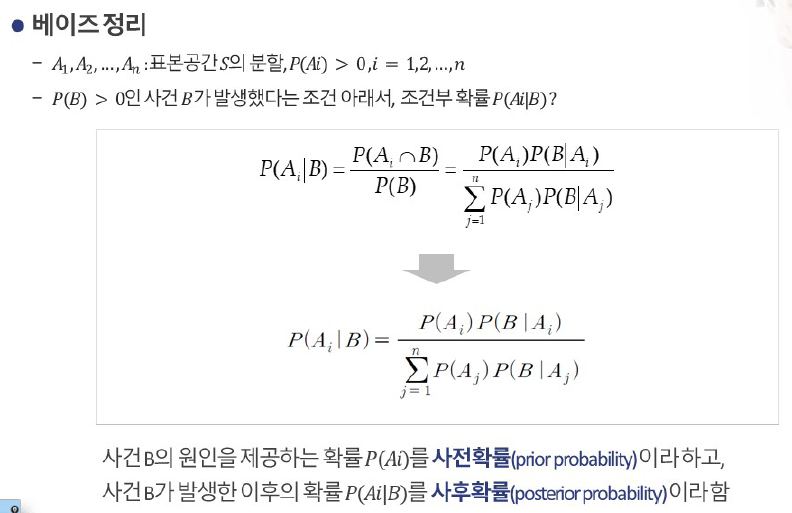

베이즈 정리 예제 계산 1
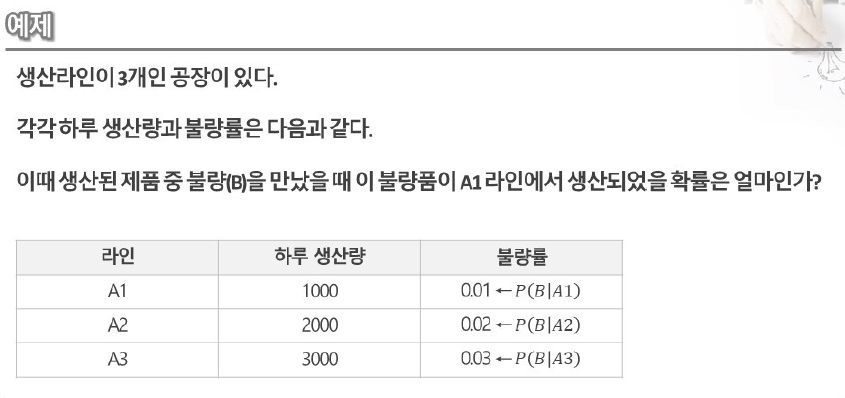
1) P(B) 구하기
P(B) = {P(B | A1) * P(A1)} + {P(B | A2) * P(A2)} + {P(B | A3) * P(A3) } = 0.02
P(A1) = 1/6, P(A2) = 2/6, P(A3) = 3/6
2) P( A1 | B ) 전개하기
P(A1 | B) = P(A1 교집합 B) / P(B) = P(A1) * P(B | A1) / P(B) <--여기 생각이 잘 안됨
3) 정답 : P(A1 | B)
P(A1) * P(B|A1) / P(B) = 0.0714
베이즈 정리 예제 계산 2

정답
P( B ) = P( B 교집합 A ) + P(B 교집합 Ac) = P(B | A) * P(A) + P(B | Ac) * P(Ac) = 0.0585
P( A | B) = P(A) * P( B | A ) / P(B) = 0.01 * 0.9 / 0.0585 = 0.1538
베이즈 정리 계산 팁

[ ✅ 주요 확률 분포 ]
1️⃣ 확률 변수 (Random Variable,X)
- 확률 변수는 확률적으로 변하는 값을 가지는 변수
즉, 어떤 실험을 했을 때 결과를 숫자로 표현한 것이 확률 변수 - 표본 공간의 원소를 실수로 mapping한 값
- 동전을 던졌을 때
- X = 앞면(1), 뒷면(0)
- 주사위를 던졌을 때
- X = {1, 2, 3, 4, 5, 6}
| 구분 | 설명 | 예제 |
| 이산 확률 변수 | 셀 수 있는 값(유한한 값 또는 정수) | 동전 앞/뒤, 주사위 값 (1~6) |
| 연속 확률 변수 | 특정 구간 내에서 무한한 값을 가질 수 있음 | 사람 키, 몸무게, 온도 |
2️⃣ 확률 분포 (Probability Distribution)
- 확률 분포는 확률 변수가 가질 수 있는 값과 그 값이 발생할 확률을 나타내는 방법
- 어떤 확률 변수가 어떤 확률 분포에 대응할 때, "확률 분포에 따른다" 라고 표현
- 확률 분포 함수 = 확률변수 X가 특정 실수값을 취할 확률을 X의 함수로 나타낸 것
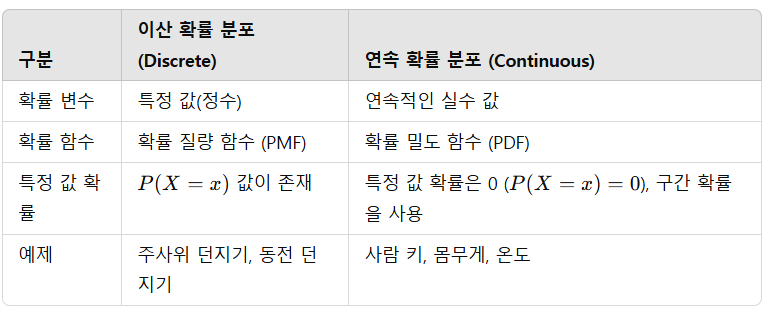
- 이산 확률 분포 (Discrete Probability Distribution)
- 확률 변수가 이산적인(정해진 값) 경우 적용
- 예: 주사위 던지기, 동전 던지기
- 연속 확률 분포 (Continuous Probability Distribution)
- 확률 변수가 연속적인 값(실수) 을 가질 경우 적용
- 예: 사람 키, 온도, 몸무게
3️⃣ 확률 분포 함수 (Probability Function)
- 확률 변수가 특정 값을 가질 확률을 정의하는 함수
확률 분포 함수는 이산 확률 변수와 연속 확률 변수에 따라 확률 질량 함수 / 확률 밀도 함수로 나뉨
🔹 이산 확률 변수 → 확률 질량 함수 (PMF, Probability Mass Function)
- 이산 확률 변수에서 특정 값이 나올 확률을 정의하는 함수.
- 예: 주사위에서 X=3X = 3이 나올 확률
- 특징
- 모든 값의 확률을 합하면 1이 됨.


🔹 연속 확률 변수 → 확률 밀도 함수 (PDF, Probability Density Function)
- 연속 확률 변수에서 특정 구간의 확률을 정의하는 함수.
- 특정한 하나의 값에 대한 확률은 0이므로 구간을 사용함.
- 확률 밀도 함수의 전체 면적(적분값)은 1이 됨.


5️⃣ 이산확률분포의 기대값과 분산

수식을 주고, 기대값과 분산값으로 풀어서 계산할 줄 알아야 한다
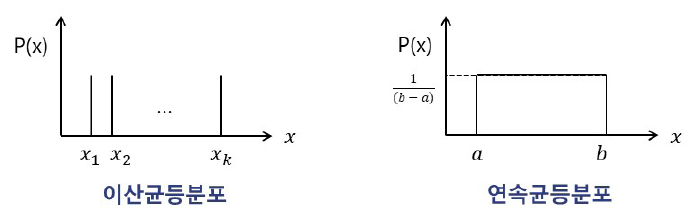
6️⃣ 균등분포 (Uniform Distribution)
- 모든 값이 같은 확률을 가지는 분포
- 이산 균등분포와 연속 균등분포로 나뉨
- 주사위 던지기, 난수 생성 등에 사용

7️⃣ 이항분포 (Binomial Distribution)
- 고정된 횟수 n 의 시행에서 특정 사건이 발생할 확률을 나타내는 분포
- 성공 또는 실패로 구분되는 실험에서 사용 (베르누이 시행의 반복, 결과가 두 종류밖에 없음)
- 예: 동전 던지기 n 번 중 앞면이 나오는 횟수
- 조건
- 시행을 n번 반복한다
- 각 시행은 성공과 실패라는 상호 배타적인 결과를 갖는다
- n번의 시행은 독립적이다
- 한 번 시행할 때 성공확률 p와 실패확률 1-p는 시행할 때마다 동일하다
- 확률변수 X는 n번 시행 중에서의 성공 횟수를 의미한다
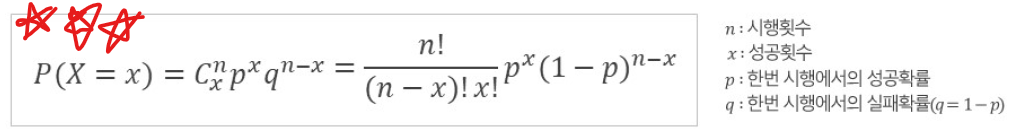

- 이항분포의 형태는 모수인 시행횟수 n과 성공확률 p의 값에 따라 결정된다
- p = 0.5에 가까우면 "n의 크기에 상관없이" 좌우대칭
- n이 크면 "p에 상관없이" 좌우대칭
- p < 1/2 이면 "오른쪽 꼬리가 긴 분포"
- p > 1/2 이면 "왼쪽 꼬리가 긴 분포"
8️⃣ 포아송 분포 (Poisson Distribution)
- 특정 시간 또는 공간에서 이벤트가 발생하는 횟수를 나타내는 분포 ( ~ 당, ~ 동안)
- 평균적으로 번 발생하는 사건을 모델링
- 예: 한 시간 동안 콜센터에 걸려오는 전화 수
- 적용 조건
- 구간마다 발생하는 사건은 독립적
- 사건 발생 확률은 "구간의 길이에 비례"
- 구간 별 확률 분포는 일정
- 람다가 커질수록, 정규 분포 형태를 띈다

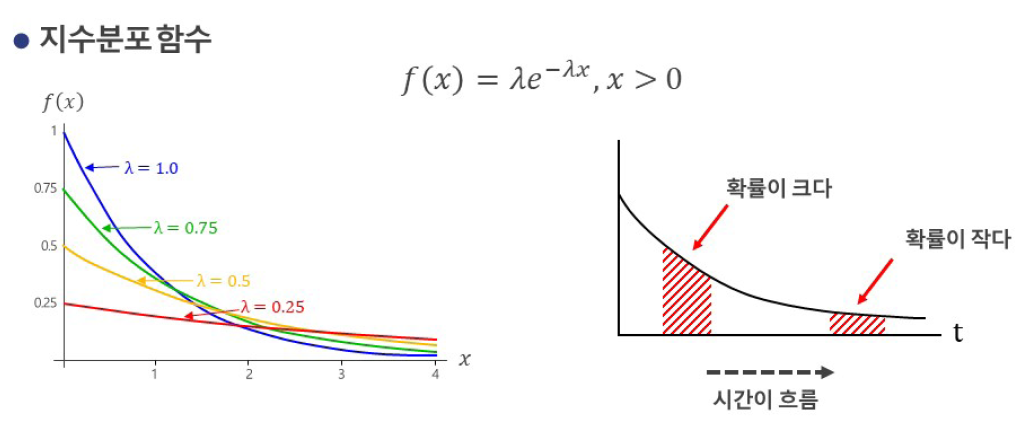
9️⃣ 지수분포 (Exponential Distribution)
- 사건 간 발생 시간(interval)이 따르는 분포(대기 시간 관련)
- 포아송 분포와 연관됨 ( 가 사건 발생률일 때, 포아송 분포는 횟수, 지수분포는 시간)
- 예: 다음 고객이 도착할 때까지 걸리는 시간
- 가 커질수록, 대기 시간이 짧아짐
- 항상 양의 값만 가지고, 평균 : 1 /
'DS > DS2' 카테고리의 다른 글
| Numpy, Pandas (0) | 2025.02.21 |
|---|---|
| 데이터 분석에 필요한 Python 기본 문법 (0) | 2025.02.21 |
| 메소드 정리 (0) | 2025.02.20 |
